4. Zerlegungsstrategie

• Partitioning
• Idee:
  • Aufbrechen des gegebenen Problems
    • in p unabhängige Teilprobleme
    • Teilprobleme haben etwa gleiche Größe
  • angewendet wenn
    • Mischen trivial
    • Zerlegen problematisch
• Beispiel: Mischen zweier sortierter Folgen
  • seriell: T*(n) = θ(n)
  • Ziel:
    • parallele Lösung
    • basierend auf Partitionierung in viele Paare von Teilsequenzen
    • gleichzeitiges Mischen der resultierenden Paare der Teilsequenzen
  • Definitionen
    • es sei S eine Menge
    • es sei X^t = (x₁,..., x_t) eine Sequenz
      • mit x_i Î S "1 ≤ i ≤ t
      • also eine Sequenz von Elementen aus S
    • es sei rank(z:X)
      • der Rang von z in X
      • = |{yÎX: y ≤ z}|
      • also die Menge der Elemente in X, die kleiner als oder gleich z sind
      • Beispiel:
        • es sei X = {2, 1, 2, 3}
        • dann ist rank(2,X) = 3
    • es sei rank(Y^s:X^t) = (r₁, ..., s_s):
      • r_i = rank (y_i,X)
      • "i Î {1, ..., s}
  • Problemstellung
    • gegeben seien Aⁿ,B^m Í S
      • Elemente in A, B seien o.b.d.A paarweise verschieden
    • gesucht ist die sortierte Folge C^m+n = (c₁, ..., c_m+n)
  • Ansätze

    • Es gilt:

      wenn An, Bm sortierte Folgen sind wenn x ÎAm È Bn und wenn Rang(x:AÈB) = i (ÎN )

      so ist x = ci

      • Beweis trivial
      • Folge: zum Mischen genügt es die Ränge rank(x: A È B) zu bestimmen
      • Beispiel:
        • X = (13, 7, 6, 5, 21)
        • Y = (4, 8, 2)
        • rank (Y, X) = (0, 3, 0)
        • Þ
          • rank (4, X È Y) = 2
          • rank (8, X È Y) = 6
          • rank (2, X È Y) = 1
    • Ansatz 1
      • Algorithmus Mischen:
        • INPUT: A^m, Bⁿ (sortiert)
        • bestimme für alle xÎA den Rang (x:B)
        • bestimme für alle xÎB den Rang (x:A)
        • dann gilt: Rang (x: A È B) = Rang (x:A) + Rang(x:B)
          • in A sind rank(x:A) Elemente kleiner oder gleich x
          • in B sind rank(x:B) Elemente kleiner oder gleich x
          • Þ in AÈB sind rank(x:A) + rank(x:B) Elemente kleiner oder gleich x
        • OUTPUT = C (sortierte Mischung von A und B)
        • Anmerkung: wenn Rang (B:A) und Rang (A:B) berechnet sind, so sind wir fertig
      • Analyse des Algorithmus:
        • Ranken von A in B
          • sei x Î A beliebig
          • sei B sortiert
          • binäre Suche nach der Position von x in B liefert den Rang von (x:B)
          • die Suchen nach den Rängen der Elemente x Î A bezüglich B können für alle x parallel erfolgen
          • binäre Suche dauert für jedes einzelne Element O(log m)
        • geht umgekehrt auch für alle Elemente von B in A

        • →

          O(log m) Zeit für A O(log n) Zeit für B

          →Zeit T(n) Î O(log(n+m))

        • WORK:
          • Annahme: n = m
          • →W(n) Î O(n log n) → Q nicht optimal
          • 
            
            Umsetzung mit mehreren Prozessoren
            (brute force) - nicht optimal
    • besser:
      • Zerlegen
        • INPUT = A = (a₁,...,a_n) , B = (b₁,...,b_m)
        • Idee:

          • Zerlegen der gegebenen Folgen in	m	Teilfolgen der Länge log m
            	log m

          • sei k(m) =	m	(o.B.d.A. ganzzahlig)
            	log m

        • Þ OUTPUT: Menge von Paaren (A_i, B_i) von Teilfolgen von A und B mit den Eigenschaften
          • Länge der Teilfolgen von B_i: |B_i| = log m
          • Σ |A_i| = n
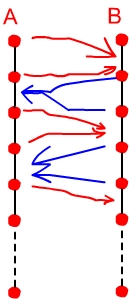
          • die Pfeile (siehe Bild) überkreuzen sich nicht
        • 
          
          
          • Elemente paarweise verschieden
          • es gibt k(m) rote Pfeile
            • rote Pfeile können sich nicht überkreuzen (Folgen sortiert)
            • zielen nicht direkt auf die a_j(i), sondern auf benachbarte Elemente
          • →pardo {rote_pfeile} - O(log n) Time
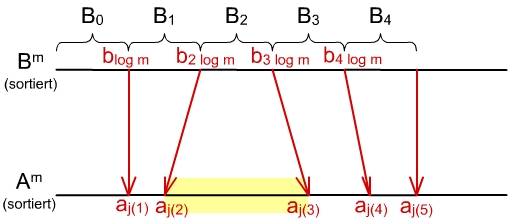
          • Def: j(i) = Rang(b_{i·log m} : A) = Rang des (i·log m)-ten Elements von B in A
          • Þ j(k(m)) = Rang(b_{k(m)·log m}:A) = Rank(b_{(m/log m)log m}:A) = rank(b_m:A)

        • k(m) =	m
          	log m
          1. j(0) = 0; j(k(m))=n 2. for i = 1 to k(m)-1 pardo      ranke bi·log m in A;      setze j(i) = rank(bi·log m:A) 3. for i = 0 to k(m)-1 pardo      Bi = (bi·log m +1, ..., b(i+1)log m)      Ai = (aj(i)+1,...,aj(i+1))

        • Analyse
          • 1. O(1) seriell
            • WORK: O(1)
          • 2. O(log n) Time

            • O(log n ·	m	) = O(m+n)
              	log m

            • denn:	m log n	≤ (n+m)
              	m

            • denn:	m log n	≤ m log (n+m) ≤ n+m log m
              	log m

            • denn	m	≤ n+m log (n+m)
              	log m

            • denn 4 < a < b Þ	a	< b log a
              	log a

            • Satz: Zerlegung funktioniert in O(log n) Zeit mit O(n+m) WORK
            • → Linear-Work + logarithmische Zeit
          • 3. O(1) Parallelzeit
      • Bemerkungen:
        • der Zerlegungsalgorithmus ist für unterschiedliche Längen angesetzt: m; n
        • der Mischalgorithmus setzt gleiche Längen m=n voraus
      • Wie Mischen?
        • da sich rote Pfeile nicht überkreuzen können jeweils die (A_i, B_i) unabhängig voneinander gemischt werden
        • 
          
          
          Problem: Mengen A_i können unterschiedlich groß (gelbe Markierung) sein
          → logarithmische Laufzeit gefährdet, da |A_i| ÏO(log n)
        • Unterscheidung
          • 1. Fall: "i |A_i| ≤ log n →O(log n) Zeit für Mischen (A_i,B_i)
          • 
            
            2. Fall: Ø 1.Fall → blaue Pfeile;
            gewährleisten Mengen, die kleiner als log m sind → O(log n) Zeit
          • geht, da weder blaue noch rote Pfeile sich kreuzen
        • Þ Mischen funktioniert in logarithmischer Zeit optimal,
          da alle zu Mischenden Abschnitte jeweils ≤ log n sind
        • WORK?
          • Zerlegen geht in O(m+n) = O(2n) = O(n), da n=m vorausgesetzt
          • Mischen braucht für jeden Teilabschnitt O(log n) Schritte, nach der

            Art der Teilung gibt es maximal	2n	Teilabschnitte Þ Work für Mischen ist ÎO( 2n log n) = O(n) Schritten möglich log n
            	log n

    • Verwendete Maschine:
      • CREW-PRAM
        • concurrent read exclusive write parallel random access machine
  • → Das Mischen zweier Sortierter Folgen funktioniert in O(log n) Zeit mit O(n) Work optimal
  • Anmerkung: dies ist nicht WT-optimal (also Zeit lässt sich noch verkürzen)