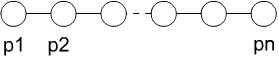I. Einleitung

serielle Algorithmen
- basieren auf
  - von-Neumann-Rechner
  - also:
    - CPU
    - Speicher
  - Instruction set:
    - Speicher lesen und schreiben
    - grundlegende arithmetische Operationen
- beurteilt nach
  Komplexität in
  - Zeit
  - Raum
    - Speicherplatz
  - Beschreibung, Beschreibungskomplexität
parallele Algorithmen
- haben verschiedene Modelle
  - beurteilt nach Kosten
    - Zeit Ä Prozessorenzahl
    - häufigster Ansatz
    - & AKL: Introduction to parallel Algorithms
  - → Modell?
  - → WORK
    - abstrakter Zugang
    - (später)
  - es ist sehr wichtig, welches Modell verwendet wird
    - Kosten sind davon abhängig
- wesentliche Punkte für parallele Rechnungen
  - computational concurrency
  - Prozessor-Allokation
    - Zuordnung der Prozessoren
      zu einzelnen Aufgaben
  - Scheduling
    - in welchen Zeitabschnitten sollen welche Aufgaben erfüllt sein?
  - Communication
    - wie kommunizieren einzelne Prozessoren miteinander?
    - wie werden Zwischenergebnisse ausgetauscht?
  - Synchronisation
    - synchrones Modell
    - asynchrones Modell
- Maße:
  - Problem P
  - serielle Komplexität T*(n)
    - Inputgröße n
    - Komplexität des besten möglichen sequentiellen
      - Algorithmus
    - wenn die Komplexität des bestmöglichen Algorithmus nicht bekannt ist,
      wird auch oft die Komplexität des besten bekannten Algorithmus verwendet
  - p - Zahl der Prozessoren
  - T_p(n) - Zeit des untersuchten parallelen Algorithmus
    bei Einsatz von p Prozessoren
  - Speedup: S_p(n) = T*(n)
    
    T_p(n)
    - ist in der Regel ≥ 1
    - gibt an, wieviel mal schneller ein paralleler Algorithmus ist
    - Ideal wäre: S_p(n) ≈ p
    - Anmerkung:
      - es ist T₁(n) die Rechenzeit auf einem "Parallelrechner" mit nur einem Prozessor
      - oft gilt T₁(n) > T*(n)
    - allgemeine Speed-Up Formel
  - Effizienz E_p(n) = T₁(n)
    
    p·T_p(n)
    - stets ≤ 1
    - gute Effizienz: Wert liegt nahe bei 1
    - T₁(n) = Paralleler Algorithmus für einen Prozessor
    - Schranke: T_∞(n)
      - diese Zeit kann nicht durch noch mehr Prozessoren verbessert werden
      - T_p(n) ≥ T_∞(n) für jeden beliebigen Wert von p
      - Þ E_p(n) ≤ T₁(n)
        
        p·T_∞(n)
      - Þ Die Effizienz eines Algorithmus nimmt mit wachsendem p schnell ab
Modelle
- DAGs
- Hypercubes / Netzwerkmodell
  - berücksichtigt das Kommunikationsmodell
  - Maße
    - Diameter = Durchmesser = maximaler Abstand zwischen einem Paar von Knoten
    - maximaler Grad = Anzahl der Kanten des Knotens mit den meisten Kanten
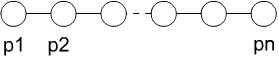
  - erster Ansatz: Prozessoren können mit Nachbarn kommunizieren
    - sehr eingeschränkt
    - Kommunikation mit 1 bis 2 Nachbarn in O(1) möglich
    - Kommunikation mit Prozessoren, die nicht direkt benachbart sind
      - geht nur über dazwischenliegende Prozessoren
      - dauert länger
    - Topologien
      - lineares Array
        
        jeder Prozessor P_i ist verbunden mit P_i-1 und P_i+1
        
        Ausnahme: Prozessoren am Rand
        
        Diameter ist = p-1
        
        maximaler Grad = 2
      - Ring
        
        lineares Array, dessen äußere Prozessoren noch verbunden werden
        
        also: P_p ist mit P₁ verbunden
  - besser:
    Kommunikation geht mit bis zu 4 Nachbarn in O(1)
    - besser
    - Kommunikation geht mit bis zu vier Nachbarn in O(1)
    - Gitter besteht aus p = m² Prozessoren
    - jeder Prozessor P_i,j ist verbunden mit den Prozessoren P_{i±1, j} und P_{i, j±1}
    - Durchmesser = √p
    - maximaler Knotengrad = 4
  - weitergedacht
    - d-dimensionaler Hypercube
    - besteht aus 2^d Prozessoren
    - Durchmesser = d = log p
    - Knotengrad ist stets d
    - Beispiel für 3-D Hypercube
      - Diameter ist log₂ p
      - Distanz = Anzahl unterschiedlicher Bits in der Prozessorzahl
      - 0-1-Codierungen → Nachbarschaften
      - Haming-Distanz zwischen zwei benachbarten Knoten = 1
    - 4-D-Hypercube
- Shared-Memory-Modell
  - (hier behandelt)
    - Grund: DAGs und Hypercubes nicht geeignet
      um allgemeine Paradigmen zu beschreiben
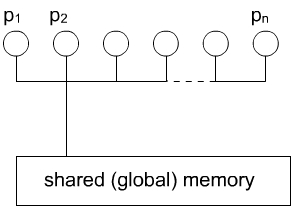
  - - Idee: Prozessoren haben einen gemeinsamen Speicher
    - lesen des Speichers kostet O(1)
    - Schreiben in Speicher kostet O(1)
    - Prozessoren können über Speicher in O(1) kommunizieren
    - keine direkte Kommunikation zwischen Prozessoren
    - können auch jweils noch zusätzlich einen eigenen Speicher haben
  - Unterscheidung
    - asynchrones Modell
      - etwas komplexer
      - es muss garantiert werden, dass Zwischenergebnisse bereitstehen, bevor auf sie zugegriffen wird
      - Q hier nicht behandelt
    - synchrones Modell
  - Beispiel Ax^{^>} = y^{^>}
    - Matrix-Vektor-Multiplikation
    - synchron parallel
    - asynchron parallelisiert
      - Prozessor 1 rechnet Zeile 1 x Vektor
      - Prozessor 2 rechnet Zeile 2 x Vektor
      - Þ einzelne Berechnungen sind unabhängig von einander
      - Problem: letzter Prozessor darf erst aktiv werden,
        wenn andere fertig sind
  - Vorteile
    - hochentwickelte Techniken und Methoden für den Umgang
      mit vielen verschiedenen Klassen von Problemen
    - löst algorithmische Details bezüglich Synchronisation und Kommunikation auf
    - erlaubt das Fokussieren auf strukturelle Eiigenschaften des Problems
    - deckt verschiedene wichtige Parameter der parallelen Berechnung ab
    - schließt explizites Verstehen der Operationen der einzenen time units ein
    - die Paradigmen auf der PRAM haben sich als robust erwiesen:
      - viele der Netzwerk-Algorithmen können direkt aus den PRAM-Algorithmen abgeleitet werden
      - viele PRAM-Algorithmen können auch auf Netzwerke mit begrenztem Knotengrad übertragen werden
Darstellung "Beschreibung" von Algorithmen nach Levels
- 1 Allgemeine Beschreibung der Wirkung des Algorithmus
- 2 Darstellung der Abfolge von time units
  - sog. Work-Time-Darstellung
- 3 Prozessorallocation → Realisierung der einzelnen Time-Units

Speedup: S_p(n) =	T*(n)
	T_p(n)

Effizienz E_p(n) =	T₁(n)
	p·T_p(n)

Þ E_p(n) ≤	T₁(n)
	p·T_∞(n)