
DAGs- directed acyclic graph
- INPUT-Knoten
- jene Knoten, deren In-Degree = 0 ist
- @ Eingaben
- im Bild: a1, a2
- innere Knoten
- haben Indegree = 2
- im Bild: +
- OUTPUT-Knoten
- haben Out-Degree = 0
- @Ausgaben
- im Bild: +
- seien p Prozessoren (1,..., p) gegeben
- → in jedem inneren Knoten i eines geg. DAG können wir ein Paar (ji,ti) zuordnen
so dass zu jedem Zeitopunkt jedem Knoten ein Prozessor zugeordnet ist- 1≤ ji ≤ p
- ti ist eine Zeit
- bedeutet: zum Zeitpunkt ti wird der Knoten dem Prozessor ji zugewiesen
- 1. wenn ti = tk mit i≠k → ji ≠ jk
- es ist nicht erlaubt, dass ein Prozessor zu einem Zeitpunkt zwei Operationen ausführt
- 2. Wenn (j,k) ein Bogen (gerichtete Kante) im Graph ist, so sei tk ≥ tj+1
- bedeutet: führe eine Berechnung erst aus, wenn benötigte Zwischenergebnisse vorliegen
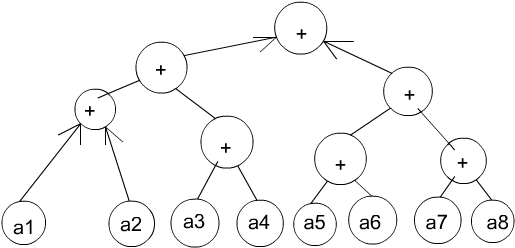
Beispiel- den Input-Knoten (unten) wird kein Prozessor zugewiesen
- hier sind 4 Prozessoren sinnvoll
- Annahme für Performance-Überlegungen:
der Datenaustausch verursacht keine weiteren Kosten Þ logarithmische Laufzeit bei n Prozessoren für n Input-Knoten 2
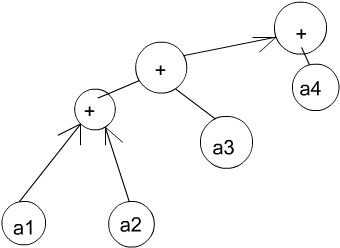
→schlechter:
· lineare Laufzeit
· unabhängig von der Zahl der Prozessoren
- → in jedem inneren Knoten i eines geg. DAG können wir ein Paar (ji,ti) zuordnen
- Knotenmenge N
- Die einzelnen Knoten sind i Î N
- (ji;ti): Prozessor ji ist dem Knoten i zugeordnet zum Zeitpunkt ti
- Þ jeder Knoten i aus N wird zu einem bestimmten Zeitpunkt von einem bestimmten Prozessor bearbeitet
- Ablaufplan (shedule)
- ist eine Folge (ji;ti) (i Î N) mit Bedingungen:
- 1: zum gleichen Zeitpunkt kann ein Prozessor nur einem Knoten zugeordnet sein
- 2: ein Prozessor für einen Knoten einer gerichteten Kante kann erst aktiv werden;
wenn die zuführenden Knoten bereits von Prozessoren verarbeitet wurden - sind diese erfüllt, spricht man von einem Ablaufplan
- Tp(n) = minAblaufpläne mit p Prozessoren(maxiÎN(ti))
ist die Rechenzeit mit p Prozessoren- also: Minimum über alle möglichen Ablaufpläne, die von p Prozessoren umgesetzt werden
- Ansätze

schlechter Ansatz (lineare Laufzeit)
besser (logarithmische Laufzeit)
- Kosten C(n) := P(n) · Tp(n)
- p=P(n) - Zahl der eingesetzten Prozessoren
- Kosten = Produkt von Prozessoranzahl und Prozessorzeit
- ein paralleler Algorithmus kann einfach in einen sequentiellen konvertiert werden:
- es soll einfach ein einzelner Prozessor nacheinander die P(n) Prozessoren simulieren
- die Laufzeit ist dann O(C(n)) mit O(P(n)) für jeden der T(n) parallelen Schritte
- ebenso ist es möglich, den Algorithmus für P(n) Prozessoren mit p ≤ P(n) Prozessoren zu simulieren:
- im ersten Schritt werden die ersten 1, 2, ..., p Prozessoren simuliert
- im zweiten Schritt die Prozessoren p+1, p+2, ..., 2p
- usw.
die benötigte Zeit ist dann O( T(n)P(n) ) p
- bei p > P(n) kann man einfach T(n) erhalten, indem man nur P(n) Prozessoren verwendet
- folgende Möglichkeiten zur Messung der Performance von parallelen Algorithmen sind gleichwertig:
- P(n) Prozessoren und T(n) Zeit
- C(n) = P(n)T(n) Kosten und T(n) Zeit
O( T(n)P(n) ) Zeit für eine Zahl p ≤ P(n) p O( C(n) + T(n)) Zeit für eine beliebige Zahl von p Prozessoren p
- ist eine Folge (ji;ti) (i Î N) mit Bedingungen:
- Bemerkung: ein einzelner Prozessor kann in P(n) Zeit
einen Arbeitstakt der P(n) Prozessoren simulieren- jeder der P(n) Prozessoren mach zu jeder time unit einen Takt
- → ein Prozessor, der in jeder Unit einen Takt macht,
kann in P(n) Zeit einen Takt von P(n) Prozessoren simulieren - → Die Kosten eines parallelen Algortihmus können
dass serielle Optimum einer algorithmischen
Aufgabe nie untertreffen - → NP-vollständige Probleme lassen sich auch im parallelen nicht effizient lösen
- np-vollständig
- Beispiel: Sortieren
- geht im seriellen in Ω(n log n)
- im parallelen ist O(log n) möglich
- dazu werden jedoch n Prozessoren benötigt
- Þ Kosten n·log n

shared memory modell- Zeit, die zum Kommunizieren nötig ist wird ignoriert
- ist nicht zu vernachlässigen
- aber: für den Vergleich verschiedener Algorithmen nicht so wichtig
- Algorithmen, die bei Vernachlässigung der Datenaustauschzeit optimal sind,
sind auch dann noch gut, wenn die Kommunikation beachtet wird

Beispiel: Matrixmultiplikation
Partitionierung- bei dieser Variante kann das Ergebnis (Addition der Teilergebnisse)
erst berechnet werden, wenn alle Teilergebnise vorliegen
- PRAM
- Eine PRAM ist eine synchrone shared-memory-Maschine
- global read (X,Y)
- Daten X aus shared memory
- werden in lokale Variable Y übertragen
- global write (U,V)
- lokale Daten U
- werden in shared Memory V (gobal) übertragen
- Algorithmus Summe
- INPUT := Array A[i] = A[1]...A[2k]
- i = Prozessornummer
- Array A der Länge n=2k
- funktioniert auch mit weniger als n Prozessoren
- n ist die maximale noch sinnvolle Anzahl von Prozessoren
- gewünschter OUTPUT := Summe S der Werte aus A
- Programm für Prozessor i
-
1 globalRead(A[i],a)
2 globalWrite(a,B[i])
3 for k:=1 to log(n) do
4 if i≤ n then 2k 5 globalRead(B[2i-1],x)
6 globalRead(B[2i],y)
7 z:=x+y
8 globalWrite(z;B[i])
9 if i=1 then globalWrite(z;S)
end for- ist Programm für einzelnen Prozessor i
- erste 2 Zeilen
- Kopieren des Inputarrays A (i-weise) in ein Array B
- "Rückhalten" für rekursiven Algorithmus
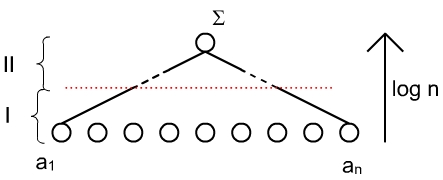
Zeile 3;4:
nötige Prozessorzahl wird im
Baum mit wachsender Höhe geringer!auf Höhe k werden n Prozessoren benötigt 2k
- kurz:
1 B(i):=A(i)
2 for A:=1 to log(n) do
3 if i≤n/2k
4 setze B(i)=B(2i-1)+B(2i)
5 if i=1
6 setze S=B(1)
gleicher Algorithmus, ohne Aufschreiben der Kommunikation mit dem shared Memory - Kosten C(n) := P(n) · Tp(n)
- p=P(n) - Zahl der eingesetzten Prozessoren
- Kosten = Produkt von Prozessoranzahl und Prozessorzeit
- ein paralleler Algorithmus kann einfach in einen sequentiellen konvertiert werden:
- es soll einfach ein einzelner Prozessor nacheinander die P(n) Prozessoren simulieren
- die Laufzeit ist dann O(C(n)) mit O(P(n)) für jeden der T(n) parallelen Schritte
- ebenso ist es möglich, den Algorithmus für P(n) Prozessoren mit p ≤ P(n) Prozessoren zu simulieren:
- im ersten Schritt werden die ersten 1, 2, ..., p Prozessoren simuliert
- im zweiten Schritt die Prozessoren p+1, p+2, ..., 2p
- usw.
die benötigte Zeit ist dann O( T(n)P(n) ) p
- bei p > P(n) kann man einfach T(n) erhalten, indem man nur P(n) Prozessoren verwendet
- folgende Möglichkeiten zur Messung der Performance von parallelen Algorithmen sind gleichwertig:
- P(n) Prozessoren und T(n) Zeit
- C(n) = P(n)T(n) Kosten und T(n) Zeit
O( T(n)P(n) ) Zeit für eine Zahl p ≤ P(n) p O( C(n) + T(n)) Zeit für eine beliebige Zahl von p Prozessoren p
-
- INPUT := Array A[i] = A[1]...A[2k]
- Algorithmus Summe
(Programm für Prozessor-Allocation)- INPUT:
- An: n=2k
- Prozessoranzahl p=2q ≤ n
- s: 1 ≤ s ≤ p ist die Prozessornummer
- OUTPUT: S (Summe) = \sum{i=1,n}A[i]
- Pseudocode
- 1 for j:=1 to l do setze B[l*(s-1)+j] := A[l*(s-1)+j]
2 for h:=1 to log(n) do // für jede "Ebene" im Baum
2a if (k-h-q≥0) then // wenn Prozessor in einer "Ebene" noch mehrere Berechnungen ausführen muss
for j:=2k-h-q(s-1)+1 to 2k-h-q*s do setze B[j]:=B[2j-1]+B[2j]
2b elseif (s≤2k-h) then setze B[j]:=B[2j-1]+B[2j] // wenn Prozessor s je nur noch eine Aufgabe erfüllen muss
3 if (s=1) then S:=B[1] // Prozessor erhält am Ende das Endergebnisl= n ist die Größe des Teilproblems, dass einer der Prozessoren am Anfang lösen muss p - wenn für (obiges Beispiel) weniger als 8 Prozessoren verwendet werden,
so muss die Arbeit am Anfang auf die vorhandenen Prozessoren aufgeteilt werden (es gilt k-h-q ≥ 0) n ≥ p 2k
- 1 for j:=1 to l do setze B[l*(s-1)+j] := A[l*(s-1)+j]
- INPUT:
- Darstellung / Beschreibung von Algorithmen in "levels"
- 1. Level : allgemeine Beschreibung der Wirkung des Algorithmus
- 2. Level
- Darstellung als Abfolge von time units
- jede time-unit kann eine beliebige Anzahl gleichzeitiger Operationen enthalten
- verbirgt spezifische algorithmische Dateils
- upper level
- 3. Level:
- Prozessor-Allokation / Realisierung der einzelnen time units
- lower level
- Erweiterung der Notation
- paralleles Abarbeiten
- for i=1..n pardo
- for l ≤ i ≤ u pardo
- die jeweils darauf folgenden Statements können für die
verschiedenen Werte von i gleichzeitig ausgeführt werden
- Darstellung des Algortihmus
Summe in zwei Levels- oberes:
- hier wird die generelle Vorgehensweise beschrieben
- unteres:
- beschreibt den Algorithmus als Abfolge von sog. Zeiteineiten
die im Prinzip in einem Arbeitstakt gelößt werden können - als Menge von Operationen, die gleichzeitig ausführbar sind
- @ Scheduling
- → "time units"
- beschreibt den Algorithmus als Abfolge von sog. Zeiteineiten
- Algorithmus Summe
(Beschreibung im upper level)- INPUT = n=2k Zahlen im Array A
- diese Version des Algorithmus macht keine Aussage
über die Anzahl der Prozessoren oder die Allokation zu diesen
- diese Version des Algorithmus macht keine Aussage
- OUTPUT := Summe S=\sum{i=1;n}A(i)
1 for 1≤i≤n pardo
2 setze B[i]=A[i] //eine time-Unit
3 for h:=1 to log(n) //do Ebenen nacheinander
4 for 1 ≤ i ≤ n pardo 2h 5 B[i]:=B[2i-1]+B[2i] innerhalb der Ebene parallel! - Algorithmus SummeW
- diese Beschreibung ist nicht nur für einen Prozessor
- Þ man sieht sofort, was gleichzeitig geschehen kann, und was nacheinander geschehen muss
- Abfolge von time units: innerhalb einer time unit können (ein oder) mehrere Berechnungen parallel ablaufen
- aber: die Werte einer Schicht können erst berechnet werden,
nachdem die darunter liegende Schicht berechnet wurde
- INPUT = n=2k Zahlen im Array A
- Problem: wie misst man den Aufwand / die Zeit?
- oberes:
- Definition: Work
- WORK(n) := Anzahl der insgesamt auszuführenden Einzeloperationen
- abgekürzt mit W(n)
- es gilt: W(n) ≤ C(n)
- serielle Komplexität ≤ W(n) ≤ C(n)
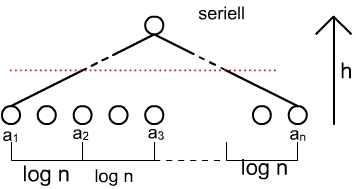
anschaulich→Einsatz von n Prozessoren für die Berechnung der log n langen Teilsummen log(n) 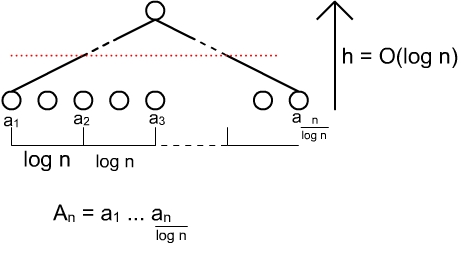
- →Kosten von SummeW sind W(n) ÎO(n)
- W(n) = C(n), wenn alle Prozessoren in jedem Takt aktiv sind
- W(n) ist unabhängig von der Prozessoranzahl
- Kosten sind aber unterschiedlich:
C(n) = n log n mit n Prozessoren
n (= log n· n ) mit n Prozessoren logn log n -
Grund: bei Verwendung von nur n Prozessoren sind weniger Prozessoren idle log n
-
- Work für den Algorithmus Summe:
- es gibt 2 + log n time-units
- erste: n Operationen
j-te "verbraucht" n Operationen für 2 ≤ j ≤ 1+ log n 2j-1 - in der letzten time-unit findet lediglich eine Operation statt
die work ist damit W(n) = n + Σ log n n + 1 Î O(n) j=1 2j
- es gibt 2 + log n time-units
- Kosten C(n) := P(n) · Tp(n)
- p=P(n) - Zahl der eingesetzten Prozessoren
- Kosten = Produkt von Prozessoranzahl und Prozessorzeit
- ein paralleler Algorithmus kann einfach in einen sequentiellen konvertiert werden:
- es soll einfach ein einzelner Prozessor nacheinander die P(n) Prozessoren simulieren
- die Laufzeit ist dann O(C(n)) mit O(P(n)) für jeden der T(n) parallelen Schritte
- ebenso ist es möglich, den Algorithmus für P(n) Prozessoren mit p ≤ P(n) Prozessoren zu simulieren:
- im ersten Schritt werden die ersten 1, 2, ..., p Prozessoren simuliert
- im zweiten Schritt die Prozessoren p+1, p+2, ..., 2p
- usw.
die benötigte Zeit ist dann O( T(n)P(n) ) p
- bei p > P(n) kann man einfach T(n) erhalten, indem man nur P(n) Prozessoren verwendet
- folgende Möglichkeiten zur Messung der Performance von parallelen Algorithmen sind gleichwertig:
- P(n) Prozessoren und T(n) Zeit
- C(n) = P(n)T(n) Kosten und T(n) Zeit
O( T(n)P(n) ) Zeit für eine Zahl p ≤ P(n) p O( C(n) + T(n)) Zeit für eine beliebige Zahl von p Prozessoren p
- Definition: Work
- WORK(n) := Anzahl der insgesamt auszuführenden Einzeloperationen
- abgekürzt mit W(n)
- es gilt: W(n) ≤ C(n)
- serielle Komplexität ≤ W(n) ≤ C(n)

anschaulich→Einsatz von n Prozessoren für die Berechnung der log n langen Teilsummen log(n) 
- →Kosten von SummeW sind W(n) ÎO(n)
- W(n) = C(n), wenn alle Prozessoren in jedem Takt aktiv sind
- W(n) ist unabhängig von der
- Prozessoranzahl
- Kosten sind aber unterschiedlich:
C(n) = n log n mit n Prozessoren
n (= log n· n ) mit n Prozessoren logn log n -
Grund: bei Verwendung von nur n Prozessoren sind weniger Prozessoren idle log n
-
Speedup: Sp(n) = T*(n) Tp(n) - ist in der Regel ≥ 1
- gibt an, wieviel mal schneller ein paralleler Algorithmus ist
- Ideal wäre: Sp(n) ≈ p
- Anmerkung:
- es ist T1(n) die Rechenzeit auf einem "Parallelrechner" mit nur einem Prozessor
- oft gilt T1(n) > T*(n)
- allgemeine Speed-Up Formel
Effizienz Ep(n) = T1(n) p·Tp(n) - stets ≤ 1
- gute Effizienz: Wert liegt nahe bei 1
- T1(n) = Paralleler Algorithmus für einen Prozessor
- Schranke: T∞(n)
- diese Zeit kann nicht durch noch mehr Prozessoren verbessert werden
- Tp(n) ≥ T∞(n) für jeden beliebigen Wert von p
Þ Ep(n) ≤ T1(n) p·T∞(n) - Þ Die Effizienz eines Algorithmus nimmt mit wachsendem p schnell ab
- nicht wirklich ein Theorem J
- Gegeben sei ein Algorithmus mit W(n) WORK in T(n) time-units
- meist funktioniert folgendes:
- wir können diesen Algorithmus mit p Prozessoren in
Tp(n) ≤ \floor{ W(n) } + T(n) parallelen Schritten simulieren p - Beweis:
- Es sei Wi(n) die Zahl der Operationen in der i-ten Zeiteinheit (im Sinne der Time-Units)
- mit 1 ≤ i ≤ T(n)
jeder Schritt Wi kann in \ceil{ Wi(n) } Parallel-Schritten mit p Prozessoren realisiert werden p - denn: in jedem Schritt mit p Prozessoren können p der W(n) übrigen Operationen ausgeführt werden
- erfolgreiche Simulation:
Zahl der Takte ≤ \sum{i}\ceil{ Wi(n) } ≤ \sum{i}\floor{ Wi(n) +1} ≤ \floor{ W(n) }+T(n) p p p
- → Mindestrechenzeit für Algorithmus ist also Zahl der Time-Units
- es sei T*(n) die sequentielle Komplexität eines Problems Q: en Algorithmus für Q läuft in O(T*(n))
- Def.: Ein paralleler Algorithmus heißt optimal,
wenn W(n) von der Größenordnung her mit
T*(n) übereinstimmt.- W(n) Î Θ(T*(n))
- unabhängig von seiner Laufzeit!
- T*(n) = serielle Komplexität
- Beispiel:
- klassisches serielles Mergesort
- Prozessoranzahl = 1
- Arbeitstakte = n log n
- Þ kann auf einer p-Prozessor PRAM-Maschine simuliert werden:
Tp(n) = O( T*(n) + T(n)) p - Theorem von Brent
Þ Speedup Sp(n) = Ω( T*(n) ) = Ω( pT*(n) ) T*(n)+pT(n) T*(n) + T(n) p Þ optimaler Speedup (Sp(n) = Θ(p)) für p = O( T*(n) ) T(n)
- Ein paralleler Algorithmus heißt streng optimal (WT-optimal), wenn
· er optimal ist und wenn
· es keinen schnelleren optimalen Algorithmus gibt- → Mergesort ist nicht streng optimal!
- in der Regel sucht man nach streng optimalen Algorithmen
(aber nicht immer) - Laufzeit eines streng optimalen Algorithmus repräsentiert die maximale Geschwindigkeit,
die ohne Verlust bei der Gesamtzahl der Operationen erreicht werden kann