List-Ranking

• Beispiel:
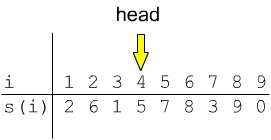
  • Liste aus 9 Knoten
  • gegeben über Array
  • 
    
    
• Algorithmus List Ranking
  (Basisalgorithmus)
  • verwendet Pointer Jumping Technik
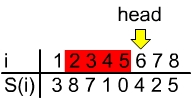
  • INPUT: Liste (siehe Beispiel oben)
  • OUTPUT: "i (1 ≤ i ≤ n): Abstand R(i) vom Ende der Liste
  • begin
  • for 1 <= i <= n pardo
    • if s(i)≠0 then R(i):=1 else R(i):=0
  • for 1 <= i <= n pardo
    • setze Q(i) := S(i)
    • while Q(i)≠0 und Q(Q(i)) ≠ 0 do
      • R(i):=R(i)+R(Q(i))
      • Q(i):=Q(Q(i))
  • end
  • dieser Algoritmus entspricht dem
    • Algorithmus Parallel Prefix (für Bäume)
    • Abwandlungen:
      • der Endknoten ist nicht durch einen Zeiger auf sich selbst markiert,
        sondern durch einen Zeiger auf 0
      • im ersten Schritt werden für alle Knoten (mit Ausnahme der Wurzel) die "Gewichte" auf 1 gesetzt
      • im zweiten Schritt werden die Knotengewichte &@Pfadlängen addiert und die Pfade "abgekürzt"
  • Analyse
    • O(log n) Time
    • O(n log n) WORK
    • Q nicht optimal, da im seriellen in linearer Zeit möglich
• Idealsituation wäre:
  • 
    
    
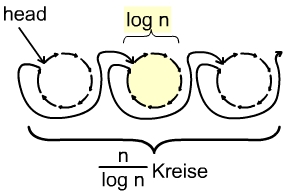
  • dann könnten die Kreise parallel mit dem
    List-Ranking-Basisalgorithmus abgearbeitet werden
    • Þfür jeden Kreis log n Zeit
    • Þ für jeden Kreis log n Work
    • Þ für alle Kreise zusammen log n Zeit

    • Þ für alle Kreise zusammen O(	n	log n) = O(n) Work
      	log n

  • für	n	Verbindungen der Kreise:
    	log n

    • es sei m :=	n
      	log n

    • dann braucht man für die Verbindungen

      O(log m) = O(log	n	) = O(log n - log log n) Î O(log n) Zeit
      	log n

    • dann braucht man für die Verbindungen

      O(m log m) = O(	n	log n ) = O( n (log n - log log n)) Î O( n log n) = O(n) Work log n log n log n
      	log n

  • → insgesamt lineare Zeit
  • Problem ist in der Regel nicht so gegeben! → naiver Ansatz funktioniert nicht!
• Trotzdem möglich mit 3 Schritten

  • 1. Reduziere die Liste, bis nur	n	Knoten bleiben
    	log n

  • 2. wende den Basisalgorithmus (List Ranking) auf die Reduzierte Liste an
    • → O(log n) TIME
    • → O(n) WORK
  • 3. Stelle die ursprüngliche Liste wieder her und bestimme
    den Rang aller ursprünglichen Elemente
• Frage: wie reduzieren?
  • Finden einer unabhängigen Menge
    • Definition: Eine Menge I von Knoten einer Liste L heiße unabhängig,
      wenn für alle iÎI gilt: S(i) Ï I
      • Beispiel:
        • 
          
          
        • 
          
          
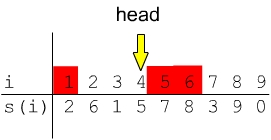
        • rot markierte = unabhängige Elemente
      • Idee: die Knoten einer unabhängigen Menge lassen sich parallel entfernen
    • Problem: wie unabhängige Menge finden? (Symmetry breaking!)
      • durch 3-Färbung
      • Elemente der unabhängigen Menge = Menge der Minimalfarben
    • Problem: finden einer hinreichend großen unabhängigen Menge
    • Lemma:
      • Sei eine k-Färbung der Knoten der Liste Lⁿ gegeben
      • die Menge der lokalen Minima/Maxima (Farben werden durch Zahlen repräsentiert)

        ist eine unabhängige Menge der Größe Ω(	n	)
        	k

      • Beweis:
        • seien u, v zwei "benachbarte" lokale Minima
          • Þ u, v sind nicht adjazent
          • 
            
            
        • zwischen u und v sind maximal 2k-3 Knoten!
          • das sind bei 3 Farben also 3 Stück :)
          • Beweis:
            • es gebe k Farben
            • es sei min die kleinste und max die größte Farbe
            • 
              
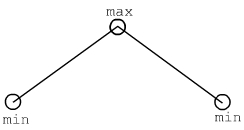
              um die maximale Distanz zwischen zwei lokalen Minima zu erhalten,
              setze man je ein min nach außen und ein max in die Mitte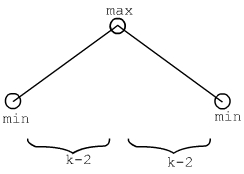
            • 
              
              zwischen dem linken min und dem max sowie
              dem rechten min und dem max liegen jeweils k-2 andere Farben
            • damit liegen zwischen den Minima genau 2(k-2)+1 = 2k - 4 +1 =2k-3 Farben
        • sei m ≤ 2k-3 die maximale Distanz zwischen zwei lokalen Minima

        • Das Intervall n wird damit in mindestens	n	Teile geteilt
          	m

        • Þ	n	≥ n Î Ω( n ) k 2k-3
          	m

      • Die Menge der lokalen Minima kann in O(1) TIME mit O(n) Work aus der k-Färbung bestimmt werden
    • Analyse
      • O(1) TIME
      • O(n) WORK
  • Pseudocode Reduktionsalgorithmus
    • INPUT:
      • Arrays S, P (Nachfolger und Vorgänger) für Liste Lⁿ
      • unabhängige Menge I: P(i)≠ 0, S(i) ≠ 0 "i: R(i)
        • Beim ersten Aufruf des Algorithmus ist

          R(i) :=

          1, falls Knoten nicht Ende der Liste 0, falls Knoten = Endknoten

        • bei weiteren Aufrufen ändert sich das R-Array
    • OUTPUT: reduzierte Liste mit den aktualisierten R-Werten
    • begin
    • ordne den Elementen der unabhängigen Menge Seriennummern N[i] zu
      • // &@ Nummerierung der roten Elemente
      • 
        
        // im Beispiel: N(1) = 1; N(5) = 2; N(6) = 3
      • // benutzen von Parallel-Präfixsumme
        • 
          
          Präfixsummenproblem
      • // →O(log n) TIME, O(n) WORK
    • für alle iÎI pardo
      • U[N[i]] = (i; S[i]; R[i])
        • Speichern von wichtigen Informationen über N[i]
      • R[P[i]] := R[P[i]]+R[i]
      • S[P[i]]:=S[i]
        • // entfernen
      • P[S[i]]:=P[i]
        • // entfernen
      • 
        
        // Ergebnis eines solchen Schrittes
      • dieser Schritt entspricht einem Schritt bei
        • Algorithmus Parallel Prefix (für Bäume)
        • jedoch werden nur Knoten der unabhängigen Menge "überbrückt"
    • end
    • Lemma: der Reduktionsalgorithmus funktioniert in O(log n) TIME mit O(n) WORK
      • O(log n) Zeit für finden der Seriennummern mit paralleler Präfixsumme
• Algorithmus List Ranking
  • INPUT: Lⁿ : (i,S[i])
  • OUTPUT: "i: Abstand zum Ende der Liste
  • begin
  • 1. setze n₀:=n; k:=0
    • // Initialisierung
    • // k ist ein Zähler
    • // n_i ist eine fallende Zahlenfolge

  • 2. while nk >	n	do
    	log n

    • // n_k = Zahl der verblebenden Elemente nach k-ter Iteration
    • // O(log n) TIME
    • k:=k+1
      • // Iterationszähler erhöhen
    • 3-Färben und I:=Menge der lokalen Minima wählen
      • Färben von Knoten im Digraph
    • Reduktionsalgorithmus für Menge I

      • // Menge der lokalen Minima liefert I: |I| ≥	nk
        	5

    • packe die Knoten n_k in aufeinanderfolgende Speicherplätze
      • // n_k ist die Anzahl der Restknoten der reduzierten Liste
  • 3. wende Basisalgorithmus (pointer jumping) auf reduzierte Liste an
    • // O(log n) TIME
  • 4. restauriere die Ursprüngliche Liste, update die Ränge R(i)
    • das Wiedereinfügen der Knoten geht in umgekehrter Reihenfolge zum Entfernen
    • der Zeitaufwand ist der gleiche wie beim Entfernen Þ keine Veränderung der Gesamtzeit
    • beim Einfügen jedes Elementes wird unter Berücksichtigung der Distanz zu seinem Nachfolger
      die Distanz zum Listenende gesetzt
  • end
  • Analyse

    • jeder Reduktionsalgorithmus reduziert auf maximal	4	(also um mindestens 1 ) 5
      	5

    • nk+1 ≤	4	nk
      	5

    • k Iterationen: nk ≤ (	4	)k·n
      	5

      • abzusichern: (n(	4	)k ≤ n ), also ( 4 )k ≤ 1 log n 5 log n
        	5

      • es gilt: (	4	)k ≤ 1 ( 5 )k ≤ log n 4 log n
        	5

      • Þ log (	5	)k ≤ log log n
        	4

      • Þ k log (	5	) ≤ log log n
        	4

      • kÎO(log log n)

    • →(	5	)log log n ≈ log n (größenordnungsmäßig)
      	4

    • → nach O(log log n) Iterationen ist der Schritt 2 (dafür je O(log n) Zeit) abgeschlossen
    • → Time: O(log log n ·log n)
    • → WORK O(n)

      • nach jeder Iteration verringert sich die Zahl der Restelemente nach nk+1 ≤ (	4	)kn
        	5

      • Work: Σ	log log n	(	4	)k-1n Î O(n)
        	k=1		5

      • Þ optimal
• Beispiel
  • 
    
    
    • n = 8

    • →2 <	n
      	log n

  • 
    
    
  • 
    
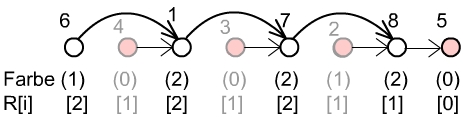
    Bestimmen einer möglichst großen unabhängigen Menge
    • gefärbte Knoten = lokale Minima = Menge I
    • 
      
      
  • entfernen der 4:
    • I={2,3,4,5}
    • N(2) = 1
    • N(3) = 2
    • N(4) = 3
    • N(5) = 4
    • U₁(N(i))
      • jetzt verwendete Schreibweise: U_x(N(i)) = U(N(i)) der x-ten Iteration
    • U₁(N(i)) = U₁(N(4)) = U₁(3) = (4,1,1)
    • 
      
      danach
  • dann: neu färben
    • 
      
      
    • 
      
      
  • →Iterationsteil abgeschlossen
  • →jetzt Pointer-Jumping
  • →Restore
• →Listranking geht in O(log log n * log n) Zeit
  • Mit wesentlich komplizierteren Techniken kann man zeigen, dass ein optimaler O(log n)-Algorithmus existiert
  • für theoretische Komplexitätsabschätzungen bentuten wir das schärfere Resultat der Bemerkung