VII. Sortieren

• Poblemstellung: siehe
  • Sortieren
• Idee
  • basierend auf
    • Mergesort
  • 
    
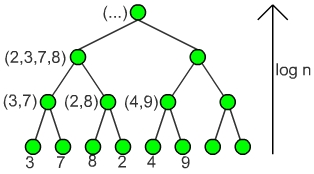
    Aufbauen eines vollständigen Binärbaums
  • Algorithmus: einfaches Mergesort
    • INPUT: n=2^l viele Werte in X
    • OUTPUT: sortierte Folge
    • begin
    • 1. for 1 ≤ j ≤ n pardo
      • L(0,j) := X(j)
    • 2. for h=1 to log n do

      • for 1 ≤ j ≤	n	pardo
        	sh

        • Merge (L(h-1,2j-1), L(h-1,2j)) zu L(h,j)
    • end
    • Analyse
      • Zeit: T(n) = O((log n) · log log n)
        • für das Mischen braucht man je Ebene log log n Time
        • siehe
          • VI. Mischen
      • WORK: O(n log n)
        • je Ebene sind n Zahlen zu Mischen
        • das parallele Mischen geht mit linearem Work
        • Þ bei log n Ebenen ergibt sich O(n log n) Work
• Besser (nach Richard Cole)
  • Ziel: O(log n) TIME optimal
  • Problem:
    • log n braucht man schon zum Ablaufen des Baumes
    • dann müsste man jeweils in O(1) mischen können
    • das geht bisher nicht!
  • Mischen mit Hilfe einer c-Decke
    • c-Decke
      • sei
        • c ÎIN
        • X eine sortierte Folge
        • Y eine sortierte Folge
      • 
        
        X ist c-Decke von Y zwischen jedem Paar aufeinanderfolgender
        Werte in X_∞ := (-∞, [X], ∞) sind höchstens c Elemente von Y
      • |{y_i | y_i Î Y: α < y_i ≤ β}| ≤ c
    • Lemmata:
      • 1.
        • Aⁿ, Bⁿ sortiert
        • sei X c-Decke von A und von B
        • Wenn Rang (X:A) und Rang(X:B) bekannt sind, so kann man A mit B in O(1) Zeit mischen
        • 
          
          
          • bekannt: Nach Voraussetzung:
          • Rang (X:A) = (r₁, .... , r_s)
          • Rang (X:B) = (t₁, .... , t_s)
          • Beweis trivial

            • xi+1 - xi ≤ c Þ

              |Ai| ≤ c |Bi| ≤ c

            • wir mischen "i parallel A_i mit B_i in O(c) Î O(1) Zeit mit O(|X|) Work
      • 2.
        • analog folgt:
        • 
          
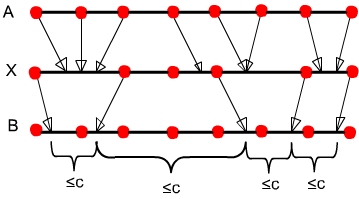
          Wenn X eine c-Decke von B ist und wenn man die Ränge Rang(A:X) und Rang(X:B) hat,
          dann kann der Rang(A:B) bestimmt werden
        • in O(1) Zeit, da für alle a_i Î A parallel
        • mit O(|A| + |X|) Work
          • O(|A|) Work, da alle Elemente in A gerankt werden müssen
          • O(|X|) Work, da ????
    • Idee:
      • die sortierte Liste L[v] der Werte für die Wurzel wird in mehreren Schritten erzeugt
      • in jedem Schritt s wird eine Näherung L_s[v] erzeugt
      • von dieser Näherung werden Samples zur nächsten Ebene "vorgeschickt"
      • mit deren Hilfe werden zwischenzeitlich wieder neue L_s+1[v] erzeugt
    • Definition:
      • Altitude eines Knotens
        • ist das Höhe eines Knotens gezählt von der tiefsten Blattebene
        • alt(v) = h(T) - level(v)
      • s seien die Schritte
      • v die Knoten
      • L[v] ist die sortierte Folge aller Blätter des Teilbames mit Wurzel v
      • L_S[v] = Approximation von L[v]
        • im Schritt s
        • noch nicht fertig
        • wird in nachfolgenden Schritten verbessert

        • L0[v] =

          Ø, wenn v ein innerer Knoten ist sonst: innerer Zahlenwert (z) in Blatt v

      • v ist voll in Schritt s L_s[v] = L[v]
      • Ziel: v voll, wenn s ≥ 3·alt(v)
        • wird dieses Ziel erreicht, dann gilt für die Wurzel r
          • alt(r) = h(T) (Höhe des Baumes)
          • Zahl der notwendigen Schritte ist 3alt(v) = 3h(T)
        • Þ dann ist v=r voll und aller Knoten enthalten ihre sortierten Listen
      • T ist voll, wenn alle Knoten v voll sind
      • der Knoten v ist aktiv (wird bearbeitet) in den Schritten s alt(v) ≤ s < 3·alt(v)
      • das c-Raster einer Liste L=(l₁, l₂, ...)
        • ist die Teilliste, die aus jedem c-ten Element besteht
        • c-Raster(L) = Raster_c(L) = (l_1·c, l_2·c, l_3·c,...)
        • Beispiel:
          • L=(4,7,8,9,11,13,15,...)
          • Raster₃(L) = (8,13,...)

      • Sample(Ls[x]) =

        Raster4(Ls[x]), wenn s ≤ 3·alt(x) Raster2(Ls[x]), wenn s = 3·alt(x)+1 Raster1(Ls[x]), wenn s = 3·alt(x)+2

        • Sample(L_s[x]) ist die Teilliste mit jedem 4. Element von L_s[x], bis x voll ist
        • danach ist L_s[x] jedes andere Element der nachfolgenden Phase 3alt(x)+1
        • dann jedes Element in Phase 3alt(x)+2
    • Algorithmus Pipelined Merge Sort
      für Schritt σ = s+1
      • INPUT:
        • für alle Knoten v eines Binärbaumes eine sortierte Liste L_s[v]
        • v voll, wenn s ≥ 3·alt(v)
      • OUTPUT: "v: sortierte Liste L_s+1[v]: v voll, wenn s+1 ≥3·alt(v)
      • es sei immer
        • u = linker Sohn von v
        • w = rechter Sohn von v
      • begin
      • for alle aktiven Knoten v pardo
        • L'_s+1[u] := Sample L_s[u]
        • L'_s+1[w] := Sample L_s[w]
        • L_s+1[v] := L'_s+1[u] È L'_s+1[w]
          • // Mischen
      • end
      • Beispiel
        • 
          
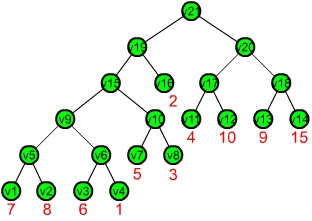
          Baum
        • Schritt 3:
          • betrachte v₅
          • v₅ aktiv alt(v₅) ≤ σ ≤ 3 alt(v₅)
            • alt(v₅) = 1
            • 3 alt(v₅) = 3
            • Þ v₅ ist zwischen Schritt 1 und 3 aktiv
          • bei σ = 3 ist v₅ voll
          • L₃[v₅] = L'₃[v₁] È L'₃[v₂] = Sample(L₂[v₁]) ÈSample(L₂[v₂]) = (7,8)
        • Schritt 11:
          • σ = 11 = s+1, d.h. s = 10
          • betrachte v₁₉
          • alt(v₁₉)=4
          • v₁₉ aktiv 4 ≤ σ ≤ 12
            • // bedeutet v₁₉ ist zwischen Schritt 4 und Schritt 19 aktiv
          • L₁₁[v₁₉] = L_s+1[v₁₉] = L' ₁₁[v₁₅] È L'₁₁[v₁₆] = sample(L₁₀[v₁₅]) È sample(L₁₀[v₁₆])
          • = Raster₂ (L₁₀[v₁₅]) È Raster₂(L₁₀[v₁₆]) = (3,6,8) È Ø = (3,6,8)
        • Schritt 12
          • σ = 12
          • 11 = 3*3+2
          • 
            
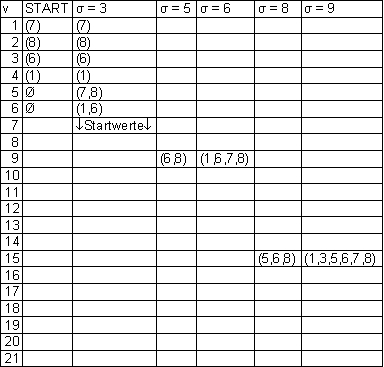
            L₁₂[v₁₉] = (1,2,3,5,6,7,8)
        • 
          
          Ablauf animiert
      • Lemmata:
        • Lemma 1
          • sei v ein beliebiger Knoten in T
          • Dann wird der Knoten v am Ende von Schritt σ = s = 3·alt(v) voll
          • Beweis
            • induktiv über alt(v)
            • 1. Fall
              • alt(v) = 0
              • L₀[v] = L[v]
            • 2. Fall
              • sei alt(v) = k > 0
              • Fall 2.1
                • v ist Blatt
                • L₀[v] = L[v]
              • Fall 2.2
                • v ist innerer Knoten
                • Þ für die Kinder u und w von v gilt: alt(u) = alt(w) = k-1
                • laut Induktionsvoraussetzung sind u, w im Schritt σ = s' = 3(k-1) voll
                • während σ = s'+1
                  • Sample L_s'[u] È Sample L_s'[w] gemischt zu L_s'+1[v]
                  • Sample L_s'[u] = Raster₄(L_s[u])
            • Schritt σ = s'+2 Þ Raster₂(L_s'[u])
            • Schritt σ = s'+3 Þ Raster₁, Sample L_s'+2 = Raster₁L[u]
            • analog für w Þ daraus folgt: L_s'+3[v] = L[v]
            • d.h. bei s' + 3 = 3k = 3·alt(v) wird v voll
        • Lemma 2
          • Sei v ein beliebiger Knoten von T und σ = 1
          • Dann gilt: |L_σ+1[v]| ≤ 2·|L_σ[v]|+4
        • Lemma 3
          • sei n_s die Zahl der Werte in den aktiven Knoten im Schritts s
          • n_s ÎO(n)
            n = Zahl der Blätter
          • Beweisskizze:

            • ns := \sum{v aktiv}|Ls[v]| = \sum{\floor{	s	} ≤ alt(v) ≤ s; } |Ls[v]|
              	3

            • \sum{v: alt(v) = \floor{	s	}; } |Ls[v]| ≤ n // Wenn ein Knoten mit alt(v) = s/3 voll wird, so kann keiner seiner Vorfahren voll sein
              	3

            • 1. Level darüber: nur	n	Knoten
              	2

            • 2. Level darüber: nur	n	Knoten
              	4

            • der Rest folgt wie bei Build-Heap Þ geht in O(n)
    • Ziel:
      • der 3. Schritt im Algorithmus (Mischen) geht in O(1) Time mit O(n_s) Î O(n) WORK
      • dieser Schritt kommt nur log n mal vor Þ gesamt O(n log n) Work, O(log n) Time
    • Technik: Merge mit c-Decke (inclusive Ranginfos)
    • Lemma 4
      • Sample (L_s-1[v]) = L'_s ist 4-Decke von Sample(L_s[v]) = L'_s+1[v]
      • Beweis
        • [a,b] sei ein Intervall mit a, b Î(-∞, L'_s[x],∞)
        • [a, b] schneidet (-∞, L'_s[v], ∞) in k Elementen, wenn |{x : xÎ(..,..,..), a ≤ x ≤ b}| = k
          • (..,..,..) = Anzahl der Elemente die in (-∞, L'_s[v], ∞) liegen
        • Behauptung (*)
          • wenn [a,b] das (-∞, L'_s[v], ∞) in k ≥ 2 Elementen schneidet,
            dann schneidet [a,b] das (-∞, L'_s+1[v], ∞) in höchstens 2·k Elementen
          • Beweis
            • Fall s=1: L'_s[v] = L'_s+1[v] = Ø
            • Induktionsvoraussetzung
              • die Behauptung gelte bis zu Schritt s-1.
              • d.h. für Schritt t < s wissen wir:
                • jedes Intervall [a',b']: a', b' Î(-∞, L'_t[v], ∞) schneidet (-∞, L'_t+1[v], ∞) in ≤ 2h Elementen
                • falls h die Anzahl ist, die zu (-∞, L'_t+1[v], ∞) gehört
            • Induktionsbehauptung für s
              • dazu [a,b]: a,b Î (-∞,L'_s[v], ∞) mit k Elementen
              • sei s ≤ 3·alt(v) (Fall B)
              • Fall A ist trivial:
                • s ≥ 3 alt(v) + 1 ≥ s-1 ≥ 3 alt(v)
                • Þ v voll in (s-1) Þ L_s-1[v] = L_s[v] = L[v] Å
                • *: |[a,b] Ç L'_s[v]| = k Þ|[a,b] Ç L'_s+1[v]| ≤ 2k
                • L'_s[v] = Sample L_s-1[v] = sample L_s[v]
                • L'_s+1[v] = sample L_s[v] (sind gleich nach Å)
                • 
                  
                  s ≤ 3 alt(v) ÞL'_s[v] = Raster₄(L_s-1[v]) Þ |[a,b] Ç L_s-1[v]| ≤ 4k-3
                • denn: L_s-1[v]
                • |[a,b] Ç L'_s[v]| ≤ k Þ |[a,b] Ç L_s[v]| ≤ 8k-2 Þ |[a,b] È L'_s+1[v}| ≤ 2k
                • 
                  
                  2p + 2q ≤ 8k + 2
                  (p+q ≤ 4k-1)
                • sei [a₁, b₁] das kleinste [a, b] enthaltende Intervall mit a₁, b₁ Î(-∞, L'_s-1[u], ∞), analog [a₂, b₂]
                • sei p die Zahl |[a₁, b₁] Ç L'_s-1[u]|
                • sei q die Zahl |[a₂, b₂] Ç L'_s-1[w]|
                • da alle Elemente verschieden sind, folgt (a, b Î {a₁, b₁, a₂, b₂}) p+q ≤ (4k - 3) + 2 = 4k -1
                  • maximal 2 Elemente zusätzlich
        • Beweis des Lemma
          • a, b Î(-∞, L'_s[v], ∞)
          • a, b seien benachbart
          • Þ |[a, b] Ç L'_s[v]| = 2 Þ |[a,b] Ç L'_s+1[v]| ≤ 2*2 = 4
          • Þ L'_s[v] ist 4-Decke von L'_s+1[v]
      • Korollar: "innere Knoten, "s ≥ alt(v):
        L_s[v] ist 4-Decke von L'_s+1[u] und L'_s+1[w] (nötig für 3. Schritt im Algorithmus)
    • Lemma 5:
      • die entsprechenden Ränge können in O(|L'_s+1[u]|+|L'_s+1[w]|) WORK und O(1) Time berechnet werden
• Analogie zum Mischen
  • seien A und B sortierte Folgen
  • Mischen:
    • anfangs:
      • Einteilen in Abschnitte der Länge log n
      • binäre Suche
      • Þ O(log n) Zeit optimal
    • später:
      • teilen in Abschnitte der Länge √n
      • Anwenden von Kruskal, siehe
        • VI. Mischen
      • O(log log n) Time
• Teile und Herrsche
  • Bestimmung der konvexen Hülle
  • Input = Menge von Punkten
  • Bilden der oberen konvexen Hülle
    • nach Kruskal
      • zwei getrennte Mengen
      • suchen der Tangente von oben her
      • Problem des Bestimmens der Kontaktpunkte der UCH
      • mittels binärer Suche
    • Teile und Herrsche
      • gegeben:
        • Mengen Sⁿ, S₁^n/2, S₂^n/2
        • allgemeiner: |UH(S₁)| = s, |UH(S₂)| = t
        • 
          
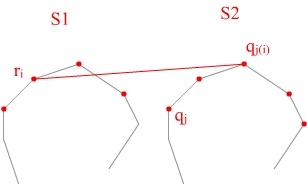
          sei r_i beliebig Î UH(S₁) (UH = upper hull)
        • Def: j(i): r_i Þ q_j(i) ist obere Tangente an UH(S₂)
      • Lemma 1:
        • sei r_i gegeben
        • q_e beliebig Î UH(S₂)
        • 
          
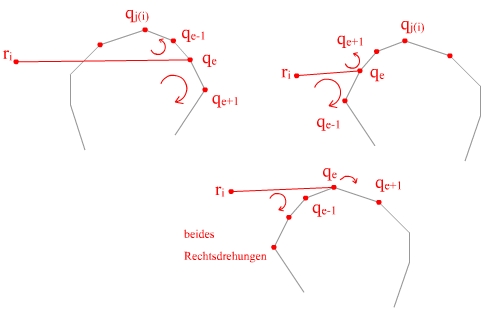
          In O(1) Zeit kann man feststellen, ob q_j(i) rechts von q_e ist oder nicht (Drehrichtungen)
      • Korollar 1
        • sei r_i beliebig Î UH(S₁)

        • Die Tangente \overline{riqj(i)} kann in O(	log t	) Zeit mit k Prozessoren errechnet werden
          	log k

        • Beweis:
          • 
            
            Strecken der oberen konvexen Hülle von S₂
          • 1 Bereich isolieren mittels Lemma 1
      • Korollar 2

        • das selbe in O(1) TIME mit k = √t Prozessoren liefert O(	log t	) = O(1) Zeit mit O(√t) Work
          	log √t

      • Lemma 2
        • sei (u,v) die gesuchte Tangente
        • (*) sei j(i) : r_i → q_j(i) gegeben

        • sei ri beliebig. Dann ist in O(1) Time eine Entscheidung möglich, ob u

          links von ri gleich ri rechts von ri

          ist

        • Beweis:
          • 
            
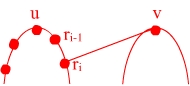
            u links von r_i ↔ r_i-1 ist oberhallb von \overline{r_iq_j(i)}
      • Lemma 3
        • = Lemma 2 ohne (*)
        • r_i beliebig. Dann ist in O(1) eine Entscheidung möglich, ob r_i links von u oder gleich r_i oder rechts von r_i
        • Beweis mittels Korollar 2:
          • q_j(i) in O(1) Zeit bestimmen
          • Lemma 2 anwenden: √t Prozessoren verwenden → Behauptung folgt
    • (Strategie für den) Algorithmus
      • 1. Zerlege UH(S₁) in √s Abschnitte der gleichen Läge √s
      • 
        
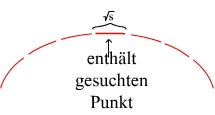
        nach Lemma 3 lässt sich mit Kruskal ein Abschnitt in O(1) Time mit O(√s·√t) Work isolieren
      • 2. symmetrisch dazu: Zerlege UH(S₂) in √t Abschnitte der Länge √t
      • nach Lemma 3* lässt sich ein Abschnitt der Länge √t, der v enthält isolieren
        • in O(1) Zeit mit O(√s·√t) WORK
        • Idee: Lemma 3* = Lemma 3, aber rechts und links vertauscht...
      • 
        
        
      • 3. Mit √s √t Prozessoren: prüfe jedes mit jedem!
        • O(1) Time
        • O(√s·√t) = O(s+t) = O(n) WORK
        • → fertig
      • Damit ist auch der Satz bewiesen: Die Bestimmung der konvexen Hülle geht in O(log n) TIME mit O(n log n) WORK
      • Bemerkung: alte Strategie lieferte O(log² n) TIME optimal